Answer:
(a)
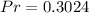
(b)
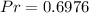
(c)

Explanation:
Given
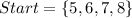 i.e. between 4 and 9
i.e. between 4 and 9
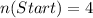
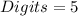
Solving (a): Probability that each of the 5 digit are different
Since there is no restriction;
The total possible selection is as follows:
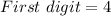 (i.e. any of the 4 start digits)
(i.e. any of the 4 start digits)
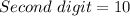 (i.e. any of the 10 digits 0 - 9)
(i.e. any of the 10 digits 0 - 9)
 (i.e. any of the 10 digits 0 - 9)
(i.e. any of the 10 digits 0 - 9)
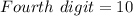 (i.e. any of the 10 digits 0 - 9)
(i.e. any of the 10 digits 0 - 9)
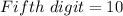 (i.e. any of the 10 digits 0 - 9)
(i.e. any of the 10 digits 0 - 9)
So, the total is:

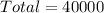
For selection that all digits are different, the selection is:
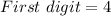 (i.e. any of the 4 start digits)
(i.e. any of the 4 start digits)
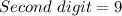 (i.e. any of the remaining 9)
(i.e. any of the remaining 9)
 (i.e. any of the remaining 8)
(i.e. any of the remaining 8)
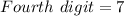 (i.e. any of the remaining 7)
(i.e. any of the remaining 7)
 (i.e. any of the remaining 6)
(i.e. any of the remaining 6)
So:
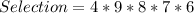
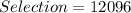
So, the probability is:
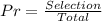
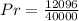
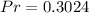
Solving (b): At least 1 repeated digit
The probability calculated in (a) is the all digits are different i.e. P(None)
So, using laws of complement
We have:
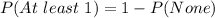
So, we have:

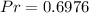
Solving (c): An expression to model the probability.
Using (a) as a point of reference, we have;
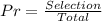
Where
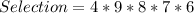 ---- for selection of 5 i.e. n = 5
---- for selection of 5 i.e. n = 5

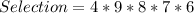
This can be rewritten as:
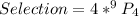
4 can be expressed as: 5 - 1
So, we have:
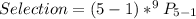
Substitute n for 5
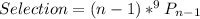


This can be rewritten as:
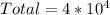

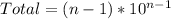
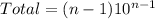
So, the expression is:
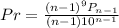

Where n represents the digit number