Answer:
Explanation:
There are several things we need to know to solve this: the perimeter formula of a rectangle, the area formula of a rectangle, and how to complete the square to find the answer. First of all, if the farmer has 148 feet of fencing to enclose 3 sides of a rectangle, the perimeter formula we need will include only 3 sides, the 2 widths and the 1 length:
P = 2w + l; solving for l and filling in our length of fencing gives us:
l = 148 - 2w
The area then for this will be:
A = (148 - 2w)(w) which is the same thing as length times width (area for a rectangle). Multiplying that out gives us:
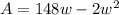 . Let's rearrange that and put it into descending order so we can complete the square on it:
. Let's rearrange that and put it into descending order so we can complete the square on it:
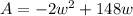
The reason we want to complete the square is because the answer that results from that will give us the dimensions of the rectangle (the width and the length) and also the area. Completing the square maximizes (or minimizes) area.
To complete the square, first factor out the -2 since the leading coefficient when you complete the square has to be a +1. When we do that we get:
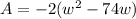 . Set it equal to 0 so we can factor it:
. Set it equal to 0 so we can factor it:
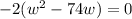
The idea now is to take half the linear term (the term stuck to the w), divide it in half, then square that number. Our linear term is 74. Half of 74 is 37, and 37 squared is 1369. So we add 1369 to both sides, the left side first:
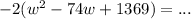
But we didn't just add in 1369. There's a -2 out front there that refuses to be ignored. It's a multiplier. What we ACTUALLY added in was -2 times 1369 which is -2738; therefore:
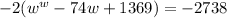
The left side can be simplified down to a perfect square binomial:
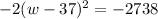
Now we'll add over the -2738:
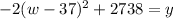 and from there determine our answer. The (w-37) term is the width of the rectangle; therefore, the length is 148 - 2(37) which is 74; the total area if the 2738. Completing the square gives us the vertex form of the parabola; the vertex is (37, 2738) where 37 is the width of the rectangle and 2738 is the max area.
and from there determine our answer. The (w-37) term is the width of the rectangle; therefore, the length is 148 - 2(37) which is 74; the total area if the 2738. Completing the square gives us the vertex form of the parabola; the vertex is (37, 2738) where 37 is the width of the rectangle and 2738 is the max area.