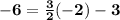Answer:
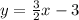
Explanation:
Step 1: Perpendicular bisector
To find the perpendicular bisector of the segment, apply the midpoint formula:
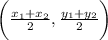
Points: {(-8, -5, (-4, 1)}
x₁ = -8 first x value
x₂ = -4 second x value
y₁ = -5 first y value
y₂ = 1 second y value
Plug the points into the formula:
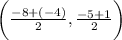
Solve:
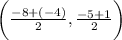
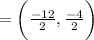
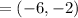
The midpoint is (-6, -2).
Step 2: Slope
To find the slope (m), apply the formula:

(point location is the same as previous step)
Plug the points into the formula; then solve:
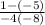
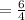
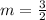
The slope is 3/2
Step 3: Solving for b
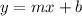
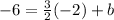
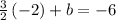
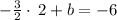
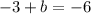
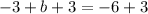
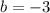
Therefore, the equation is