Question

Please help me with this!! I don’t understand it at all (trigonometry)

Answer 1

Hi there!

`\large\boxed{cos((\theta)/(2) )= (3)/(√(7))}`

`\large\boxed{tan((\theta)/(2)) = (√(5))/(3)}`

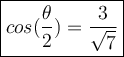
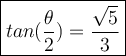
Begin by recalling that:

sin(θ) = O/H, so:

Opposite side = 3√5

Hypotenuse = 7

We can solve for the adjacent sign using the Pythagorean Theorem:

7² = (3√5)² + b²

49 = 45 + b²

b² = 4

b = 2.

Thus, cosθ = 2/ 7

Use the half angle identity to solve for cos(θ/2):

cos(θ/2) = √(1 + cosθ)

Plug in the value of cosθ:

= √(1 + 2/7) = √9/7, or 3 /√7

Thus:

`cos((\theta)/(2)) = (3)/(√(7))`

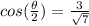
Calculate tan(θ/2) using the same process but with a different formula:

tan(θ/2) = √(1 - cosθ / 1 + cosθ)

Substitute in the value of cosθ:

tan(θ/2) = √(1 - 2/7)/(1 + 2/7)

= √(5/7)/(9/7) = √5/9 = √5/3