Question

Resolver las siguientes inecuaciones cuadráticas y presentar el conjunto solución en forma de intervalo y gráficamente. 1) X2 < 10 – 3x 2) 2x2 + 3x ≥ 2

Answer 1

Respuesta:

1) (-5,2)

2)
`(-\infty,-2]U((1)/(2),\infty)`

Explicación paso a paso:

1)

`x^(2)<10-3x`

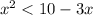
Para comenzar este problema, debemos moverlo todo al lado izquierdo de la inecuación, por lo que obtenemos:

`x^(2)+3x-10<0`

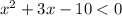
Ahora podemos factorizar el lado izquierdo para obtener:

`(x+5)(x-2)<0`

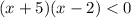
Ahora podemos cambiar el símbolo < por un = para encontrar los valores de x en los cuales la inecuación es igual a cero.

(x+5)(x-2)=0

Y luego despejamos x.

x+5=0

x=-5

y

x-2=0

x=2

Ahora construimos nuestros intervalos posibles.

`(-\infty,-5)`

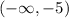
(-5,2)

y

`(2,\infty)`

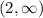
Y escogemos algunos valores de prueba. Estos nos ayudarán a determinar si cada intervalo hace que la inecuación sea verdadera o falsa.

`(-\infty,-5)`

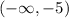
Para este intervalo escojamos -6 y evaluemoslo en la inecuación.

(x+5)(x-2)<0

(-6+5)(-6-2)<0

(-1)(-8)<0

8<0

falso, así que este intervalo no es parte de nuestra respuesta.

(-5,2)

para este escojamos x=0 y probémoslo en la inecuación.

(x+5)(x-2)<0

(0+5)(0-2)<0

(5)(-2)<0

-10<0

verdadero, así que este intervalo es parte de nuestra respuesta.

`(2,\infty)`

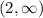
Para este escojamos 3 y probémoslo en unestra inecuación.

(x+5)(x-2)<0

(3+5)(3-2)<0

(8)(1)<0

8<0

falso, así que este intervalo no es parte de nuestra respuesta.

así que nuestra respuesta es: (-5,2)

Vea imagen adjunta para representación gráfica.

2)

`2x^(2)+3x\geq2`

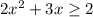
Para resolver este problema, comenzamos moviéndolo todo al lado izquierdo de la inecuación.

`2x^(2)+3x-2\geq0`

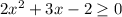
Ahora podemos factorizar el lado izquierdo de la inecuación para obtener:

`(2x-1)(x+2)\geq0`

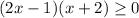
Ahora podemos cambién el símbolo ≥ por un símbolop de = para obtener los valores de x que hacen que la inecuación sea igual a 0.

(2x-1)(x+2)=0

y ahora despejamos x.

2x-1=0

`x=(1)/(2)`

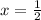
y

x+2=0

x=-2

Ahora construimos nuestros intervalos posible.

`(-\infty,-2]`

`[-2,(1)/(2)]`

y

`[(1)/(2),\infty)`

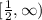
Ahora escogemos los valores de prueba correspondientes.

`(-\infty,-2]`

para este, escojamos -3 y probémoslo en la inecuación.

`(2x-1)(x+2)\geq0`

`(2(-3)-1)(-3+2)\geq0`

`(-7)(-1)\geq0`

`7\geq0`

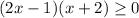
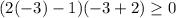
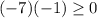
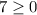
verdadero, así que este intervalo es parte de nuestra respuesta.

`[-2,(1)/(2)]`

para este, utilicemos 0 como valor de prueba.

`(2x-1)(x+2)\geq0`

`(2(0)-1)(0+2)\geq0`

`(-1)(2)\geq0`

`-2\geq0`

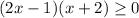
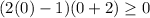
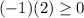
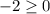
falso, así que este intervalo no es parte de nuestra respuesta.

`[(1)/(2),\infty)`

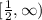
para este, utilicemos 1 como valor de prueba.

`(2x-1)(x+2)\geq0`

`(2(1)-1)(1+2)\geq0`

`(1)(3)\geq0`

`3\geq0`

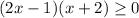
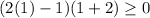
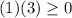
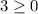
verdadero, así que este intervalo es parte de nuestra respuesta.

Así que nuestra respuesta es la unión entre los dos intervalos que resultaron verdadero, por lo que nuestra respuesta es:

`(-\infty,-2]U[(1)/(2),\infty)`

Vea la representación gráfica en la imagen adjunta.