Answer:
0.0334 = 3.34% probability that the player will make exactly 3 3-pointers and 5-free throws.
Explanation:
For each 3-pointer shot, there are only two possible outcomes. Either the player makes it, or the player does not. The same is valid for free throws. This means that both the number of 3-pointers and free throws made are given by binomial distributions.
Since 3-pointers and free throws are independent, first we find the probability of making exactly 3 3-pointers out of 10, then the probability of making exactly 5 free throws out of 10, and then the probability that the player will make exactly 3 3-pointers and 5-free throws is the multiplication of these probabilities.
Binomial probability distribution
The binomial probability is the probability of exactly x successes on n repeated trials, and X can only have two outcomes.

In which
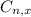 is the number of different combinations of x objects from a set of n elements, given by the following formula.
is the number of different combinations of x objects from a set of n elements, given by the following formula.
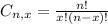
And p is the probability of X happening.
Probability of making 3 3-pointers out of 10:
The chances of a basketball player hitting a 3-pointer shot is 0.4, which means that
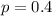 . So this is
. So this is
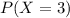 when
when
 .
.

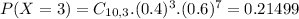
Probability of making 5 free throws out of 10:
The probability of hitting a free-throw is 0.65, which means that
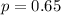 . The probability is
. The probability is
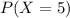 when
when
 .
.

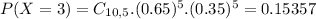
Calculate the probability that the player will make exactly 3 3-pointers and 5-free throws.
0.21499*0.15537 = 0.0334
0.0334 = 3.34% probability that the player will make exactly 3 3-pointers and 5-free throws.