Question

If it is struck by a rigid block having a weight of 550 lblb and traveling at 2 ft/sft/s , determine the maximum stress in the cylinder. Neglect the mass of the cylinder. Express your answer to three significant figures and include appropriate units.

Answer 1

This question is incomplete, The missing image is uploaded along this answer below;

Answer:

the maximum stress in the cylinder is 3.23 ksi

Step-by-step explanation:

Given the data in the question and the diagram below;

First we determine the initial Kinetic Energy;

T =
`(1)/(2)`mv²

we substitute

⇒ T =
`(1)/(2)` × (550/32.2) × (2)²

T = 34.16149 lb.ft

T = ( 34.16149 × 12 ) lb.in

T = 409.93788 lb.in

Now, the volume will be;

V =
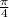`(\pi )/(4)`d²L

from the diagram; d = 0.5 ft and L = 1.5 ft

so we substitute

V =
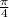`(\pi )/(4)` × ( 0.5 × 12 in )² × ( 1.5 × 12 in )

V = 508.938 in³

So by conservation of energy;

Initial energy per unit volume = Strain energy per volume

⇒ T/V = σ²/2E

from the image; E = 6.48(10⁶) kip

so we substitute

⇒ 409.93788 / 508.938 = σ²/2[6.48(10⁶)]

508.938σ² = 5,312,794,924.8

σ² = 10,438,982.5967

σ = √10,438,982.5967

σ = 3230.9414

σ = 3.2309 ksi ≈ 3.23 ksi { three significant figures }

Therefore, the maximum stress in the cylinder is 3.23 ksi