Answer:
a) p(the student did not do homework and he/she passed the course) = 0.09
b) p(the student did not do homework given that she/he passed the course) = 0.125.
Explanation:
Conditional Probability
We use the conditional probability formula to solve this question. It is

In which
P(B|A) is the probability of event B happening, given that A happened.
 is the probability of both A and B happening.
is the probability of both A and B happening.
P(A) is the probability of A happening.
a. p(the student did not do homework and he/she passed the course)
If a student does not do homework most days, the chance of passing the course is only 30%. 100 - 70 = 30% don't do homework on a regular basis.
So
0.3*0.3 = 0.09
p(the student did not do homework and he/she passed the course) = 0.09
b. p(the student did not do homework given that she/he passed the course)
Conditional probability.
Event A: Passed the course
Event B: Did not do homework.
p(the student did not do homework and he/she passed the course) = 0.09
This means that
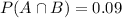
Probability that the student passes the course:
90% of 70%(do homework)
30% of 30%(do not do homework).
This means that:
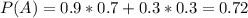
p(the student did not do homework given that she/he passed the course)
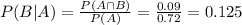
So
p(the student did not do homework given that she/he passed the course) = 0.125.