Question

A hexagonal pyramid has a volume of 144 cubic millimeters and a height of 4 millimeters. What is the area of the base of the pyramid? (Hint: Label the parts you know. Draw a picture if necessary)

This is confusing T^T

Answer 1

The area of the base of the pyramid is 109.2 mm.

Explanation:

The area of the base of a hexagonal pyramid is given by the area of a hexagon:

`A_(b) = (P*a)/(2)`

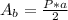
Where:

P: is the perimeter

a: is the apothem

We need to find the perimeter and the apothem.

The perimeter is equal to:

`P = 6*s`

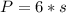
Where:

s: is the side of the pyramid

And the apothem is:

`a = (√(3))/(2)*s`

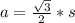
So, to calculate the apothem and the perimeter we need to calculate the side of the pyramid. We can find it from the volume of the pyramid:

`V = (√(3))/(2)*h*s^(2)`

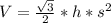
Where:

h: is the height = 4 mm

V: is the volume = 144 mm³

Then, the side is:

`s = \sqrt{(2V)/(√(3)*h)} = \sqrt{(2*144)/(√(3)*4)} = 6.5 mm`

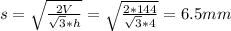
Now, we can find the perimeter and the apothem.

`a = (√(3))/(2)*s = (√(3))/(2)*6.5 = 5.6 mm`

`P = 6*s = 6*6.5 = 39 mm`

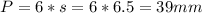
Finally, the area is:

`A_(b) = (P*a)/(2) = (39*5.6)/(2) = 109.2 mm^(2)`

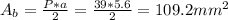
Therefore, the area of the base of the pyramid is around 109 mm.

I hope it helps you!