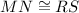Question

Hewwo!

In the figure, O is the centre of the circle , chords MN and RS are intersected at P. If OP is bisector of
`\angle` MPR , prove that : MN = RS

Answer 1

See Below.

Explanation:

Please refer to the diagram below.

We are given that O is the center of the circle, and chords MN and RS are intersected a P. OP is the bisector of ∠MPR. And we want to prove that MN = RS.

We will construct segments OK and OJ such that it perpendicularly bisects MN and RS.

Since OP bisects ∠MPR, it follows that:

`\displaystyle \angle JPO\cong \angle KPO`

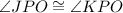
And since OK and OJ are perpendicular bisectors:

`m\angle OKP=90^\circ \text{ and } m\angle OJP=90^\circ`

Therefore:

`\angle OKP\cong \angle OJP`

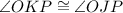
By the Reflexive Property:

`OP\cong OP`

Therefore:

`\Delta OKP\cong \Delta OJP`

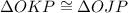
By AAS Congruence.

Hence:

`OK\cong OJ`

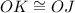
By CPCTC.

Recall that congruent chords are equidistant from the center.

Thus, by converse, chords that are equidistant from the center are congruent.

Therefore:

`MN\cong RS`

Answer 2

this is your answer look it once.