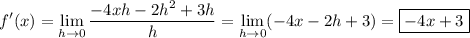Question

If f(x) = 2x^2 + 4x + 7, find f'(-5), using the definition of derivative. f'(-5) is the limit as x → -5

of the expression ?
The value of this limit is ?

Answer 1

Using the limit definition of the derivative, you have

`\displaystyle f'(-5) = \lim_(x\to-5) (f(x) - f(-5))/(x - (-5)) = \lim_(x\to-5) ((2x^2+4x+7) - 37)/(x + 5)`

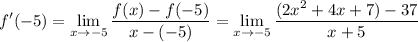
Simplify the numerator:

(2x ² + 4x + 7) - 37 = 2x ² + 4x - 30

… = 2 (x ² + 2x - 15)

… = 2 (x + 5) (x - 3)

Then

`\displaystyle f'(-5) = \lim_(x\to-5)(2(x+5)(x-3))/(x+5) = \lim_(x\to-5) 2(x-3) = \boxed{-16}`

• • •

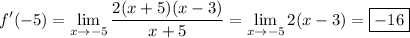
For your second question in the comments, if f(x) = -2x ² + 3x - 7, then by the definition of the derivative, you have

`\displaystyle f'(x) = \lim_(h\to0)\frac{f(x+h)-f(x)}h = \lim_(h\to0)\frac{(-2(x+h)^2+3(x+h)-7) - (-2x^2 + 3x - 7)}h`

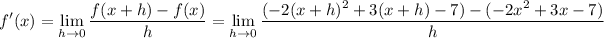
Simplify the numerator:

(-2 (x + h)² + 3 (x + h) - 7) - (-2x ² + 3x - 7)

… = (-2x ² - 4xh - 2h ² + 3x + 3h - 7) - (-2x ² + 3x - 7)

… = -4xh - 2h ² + 3h

Now compute the limit:

`\displaystyle f'(x) = \lim_(h\to0)\frac{-4xh-2h^2+3h}h = \lim_(h\to0)(-4x-2h+3) = \boxed{-4x+3}`