Question

During a game of cards, Megan divided the deck of cards into 4 equal groups. She then placed (3 of

her cards in the center of the table. If Megan now has
5 cards in her hand, how many cards were in the
entire deck?

Answer 1

Answer: 32

Step-by-step explanation: If she had 8 in her had and placed 3 cards down she would have 5 and if there were 8 cards in each group then, 8x4=32

Answer 2

There were originally 3 cards in the entire deck.

Let's denote the number of cards in the entire deck as \(D\).

Megan divided the deck into 4 equal groups, so each group has
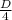`\((D)/(4)\)` cards.

She placed 3 cards in the center, and now she has 5 cards in her hand.

So, the equation representing this situation is:

`\[(D)/(4) - 3 + 5 = D\]`

Now, let's solve for \(D\):

`\[(D)/(4) + 2 = D\]`

Multiply both sides by 4 to get rid of the fraction:

`\[D + 8 = 4D\]`

Subtract \(D\) from both sides:

`\[8 = 3D\]`

Divide both sides by 3:

`\[D = (8)/(3)\]`

However, the number of cards in a deck must be a whole number, so we round up:

`\[D = 3\]`

Therefore, there were originally 3 cards in the entire deck.