Question

g Suppose, for simplicity, that three main parts of a laptop are CPU, RAM, and hard drive;so if one of theses components fails, the laptop fails. Assume that the life times of CPU, RAM, and hard drive are exponentially distributed with mean 3 years, 2 years, and 5 years, respectively. If the company that sells these laptops guarantees the replacement of any laptops that fail in the first year, anda replacement costs $500, what would be the average yearly replacement cost

Answer 1

The average yearly replacement cost is approximately $32,211,500

Explanation:

Exponential Distribution

P(X < x) = 1 - e -x/

`P(X < x) = 1 - e^{(-x)/(\mu)}`

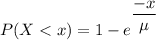
For the CPU, μ = 3 years

The probability that a CPU fails in less than 1 year is therefore;

P(C) =
`P(X < 1) = 1 - e^{(-1)/(3)} \approx 0.2835`

For the RAM, μ = 2 years

The probability that a RAM fails in less than 1 year is therefore;

P(R) =
`P(X < 1) = 1 - e^{(-1)/(2)} \approx 0.3935`

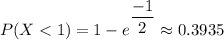
For the hard drive, μ = 5 years

The probability that a hard drive fails in less than 1 year is therefore;

P(H) =
`P(X < 1) = 1 - e^{(-1)/(5)} \approx 0.1813`

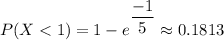
The probability that either a CPU, or a RAM or a hard drive fails in 1 year so that a replacement is required, P(C ∪ R ∪ H), is given as follows;

P(C ∪ R ∪ H) = P(C) + P(R) + P(H) - P(C∩R) - P(C∩H) - P(R∩H) + P(C∩R∩H)

∴ P(C ∪ R ∪ H) = 0.2835 + 0.3935 + 0.1813 - (0.2835 × 0.3935) - (0.2835 × 0.1813) -(0.3935 × 0.1813) + (0.2835 × 0.3935 × 0.1813) ≈ 0.64423

∴ P(C ∪ R ∪ H) ≈ 0.64423

There is a 0.64423 chance that a laptop will require replacement

For 100,000 laptops sold a year and a replacement cost of $500 per laptop, we have;

The average yearly replacement cost, 'Cost' is given as follows;

Cost = 500 × 100,000 × 0.64423 = 32,211,500

The average yearly replacement cost, Cost ≈ $32,211,500