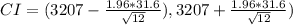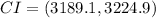Complete Question
A civil engineer is analyzing the compressive strength of concrete. Compressive strength is normally distributed with
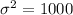 . A random sample of 12 sample specimens has a mean compressive strength of
. A random sample of 12 sample specimens has a mean compressive strength of
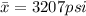 . Round your answers to 1 decimal place. (a) Calculate the 95% two-sided confidence interval on the true mean compressive strength of concrete.
. Round your answers to 1 decimal place. (a) Calculate the 95% two-sided confidence interval on the true mean compressive strength of concrete.
Answer:
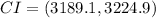
Explanation:
From the question we are told that:
Sample size

Standard deviation
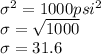
Sample mean
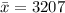
Confidence level =95%
 significance level
significance level
From table \alpha 0.05
Gives
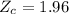
Generally the equation for confidence interval is mathematically given by