Complete Question
You and your lab partner are asked to determine the density of an aluminum bar. The mass is known accurately (to four significant figures). You use a simple metric ruler to measure its dimensions and obtain the results for Method A. Your partner uses a precision micrometer and obtains the results for Method B.
Method A (g/cm3) 2.2,2.3,2.7,2.4 Method B (g/cm3) 2.703 2.701 2.705 5.811
The accepted density of aluminum is 2.702 g/cm 3 .
(a) Calculate the average density for each method.
Should all the experimental results be included in your calculations? If not, justify any omissions.
(b) Calculate the percent error for each method’s average value.
(c) Calculate the standard deviation for each set of data.
(d) Which method’s average value is more precise? Which method is more accurate?
Answer:
a)
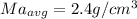
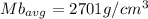
b)
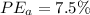

c)
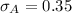
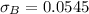
d)Method A
Step-by-step explanation:
From the question we are told that:
Method A Density values
2.7
Method B Density values
2.703,2.701,2.705,5.811
Density of aluminium
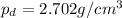 .
.
a)
Generally the average density for each method is mathematically given by
Method A
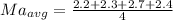
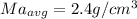
Method B

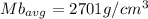
b)
Generally the equation for percentage error
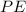 is is mathematically given by
is is mathematically given by
percent error = (measured- real)/real *100
Given real = 2.702 g/ cm3
Method A =
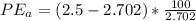
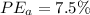
Method B =


c)
Generally the standard deviation
 for each method is mathematically given by
for each method is mathematically given by
Method A
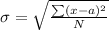
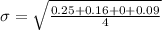
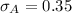
Method B
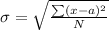
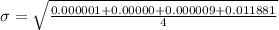
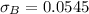
d)
Therefore with lower percentage error the method who's average value is more precise is
Method A