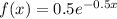Question

Suppose that two electronic components in the guidance system for a missile operate independently and that each has a length of life governed by the exponential distribution with mean 1 (with measurements in hundreds of hours). Find the probability density function for the average length of life of the two components.

Answer 1

The probability density function for the average length of life of the two components is
`f(x) = 0.5e^(-0.5x)`

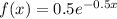
Explanation:

Exponential distribution:

The exponential probability distribution, with mean m, is described by the following probability density:

`f(x) = \mu e^(-\mu x)`

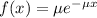
In which
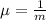`\mu = (1)/(m)` is the decay parameter.

Each missile has a length of life governed by the exponential distribution with mean 1 (with measurements in hundreds of hours). Find the probability density function for the average length of life of the two components.

2, each with mean 1 means that
`m = 2*1 = 2, \mu = (1)/(2) = 0.5`

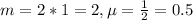
So the probability density function is:

`f(x) = 0.5e^(-0.5x)`