Question

The U.S. Energy Information Administration claimed that U.S. residential customers used an average of 10,608 kilowatt hours (kWh) of electricity this year. A local power company believes that residents in their area use more electricity on average than EIA's reported average. To test their claim, the company chooses a random sample of 187 of their customers and calculates that these customers used an average of 10,737 kWh of electricity last year. Assuming that the population standard deviation is 1220 kWh, is there sufficient evidence to support the power company's claim at the 0.05 level of significance?

1. State the null and alternative hypotheses for the test.
2. What is the test statistic?
3. Do we fail to reject or reject the null hypothesis because of sufficient or insufficient evidence?

Answer 1

The calculated value Z = 1.4460 < 1.96 at 0.05 level of significance.

The null hypothesis is accepted

A local power company believes that residents in their area use more electricity on average than EIA's reported average

Explanation:

Step(i):-

Given that the mean of the Population = 10,608 kWh of electricity this year.

Given that the size of the sample n = 187

Given that mean of sample x⁻ = 10737 kWh

The Standard deviation of the Population = 1220kWh

Level of significance = 0.05

The critical value (Z₀.₀₅)= 1.96

Step(ii):-

Null Hypothesis: H₀:μ > 10608 kWh

Alternative Hypothesis: H₁: μ < 10608kWh

Test statistic

`Z = (x^(-)-mean )/((S.D)/(√(n) ) )`

`Z = (10737- 10608 )/((1220)/(√(187) ) )`

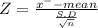
Z = 1.4460

Final answer:-

The calculated value Z = 1.4460 < 1.96 at 0.05 level of significance.

The null hypothesis is accepted

A local power company believes that residents in their area use more electricity on average than EIA's reported average.