Answer:
Since p-value ( 0.4467 ) is greater than significance level ( 0.01 )
Fail to Reject Null hypothesis H₀ at 1%.
At 1% significance level, we can conclude that, population variance is maintained at historic value.
Thus, Option ((B) At alpha = 1%, they failed to reject the null hypothesis. The variance of miles per gallon for AST72 model has not decreased from the historical value of 0.35) is the correct answer.
Explanation:
Given the data in the question;
sample size n = 24
Sample Standard deviation S = 0.58
Let δ represent the population standard deviation
so we will test;
H₀ : δ = √0.35 ≈ 0.5916
H₁ : δ < √0.35 ≈ 0.5916
Test Statistics;
we determine our test statistics as follows;
Z = [√(2(n-1))] × [ lnS - lnδ ] ~ N(0, 1 )
Now, Under H₀,
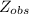 = [√(2(24-1))] × [ ln (0.58 / 0.5916) ]
= [√(2(24-1))] × [ ln (0.58 / 0.5916) ]
= 6.7823 × -0.0198026
= -0.134
From z-table;
p-value = P( z <
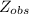 ) = p( z < -0.134 ) = 0.4467
) = p( z < -0.134 ) = 0.4467
p-value = 0.4467
Since p-value ( 0.4467 ) is greater than significance level ( 0.01 )
Fail to Reject Null hypothesis H₀ at 1%.
At 1% significance level, we can conclude that, population variance is maintained at historic value.
Thus, Option ((B) At alpha = 1%, they failed to reject the null hypothesis. The variance of miles per gallon for AST72 model has not decreased from the historical value of 0.35) is the correct answer.