Answer:
a) A sample of 198 must be drawn.
b) Smaller, because the confidence level is smaller.
Explanation:
Question a:
We have that to find our
 level, that is the subtraction of 1 by the confidence interval divided by 2. So:
level, that is the subtraction of 1 by the confidence interval divided by 2. So:
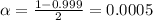
Now, we have to find z in the Ztable as such z has a pvalue of
 .
.
That is z with a pvalue of
 , so Z = 3.291.
, so Z = 3.291.
Now, find the margin of error M as such

How large a sample must be drawn so that a 99.9% confidence interval for u will have a margin of error equal to 4.1?
This is n for which M = 4.1. So

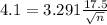
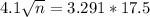
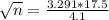
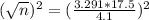
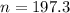
Rounding up:
A sample of 198 must be drawn.
(b) If the required confidence level were 95%, would the necessary sample size be larger or smaller?
We have that:

Solving for n

That is, n and z are directly proportion, meaning that a higher value of z(higher confidence level) leads to a higher sample size needed.
95% < 99.9%, so a smaller confidence interval.
Smaller, because the confidence level is smaller.