Question

a skier starts from rest and skis down a 82 meter tall hill labeled h1, into a valley and staught back up another 35 meter hill(labled h2). How fast in m/s is she going at the top of the 35 meter hill? Assume no friction

Answer 1

She is going at 30.4 m/s at the top of the 35-meter hill.

Step-by-step explanation:

We can find the velocity of the skier by energy conservation:

`E_(1) = E_(2)`

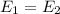
On the top of the hill 1 (h₁), she has only potential energy since she starts from rest. Now, on the top of the hill 2 (h₂), she has potential energy and kinetic energy.

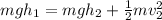`mgh_(1) = mgh_(2) + (1)/(2)mv_(2)^(2)` (1)

Where:

m: is the mass of the skier

h₁: is the height 1 = 82 m

h₂: is the height 2 = 35 m

g: is the acceleration due to gravity = 9.81 m/s²

v₂: is the speed of the skier at the top of h₂ =?

Now, by solving equation (1) for v₂ we have:

`v_(2)^(2) = (2mg(h_(1) - h_(2)))/(m)`

`v_(2) = \sqrt{2g(h_(1) - h_(2))} = \sqrt{2*9.81 m/s^(2)*(82 m - 35 m)} = 30.4 m/s`

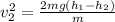
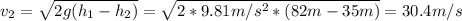
Therefore, she is going at 30.4 m/s at the top of the 35-meter hill.

I hope it helps you!