Question

1. Use the given Taylor polynomial p 2 to approximate the given quantity.

2. Compute the absolute error in the approximation assuming the exact value is given by a calculator.
Approximate e-0.07 using f(x) = e-x and p2(x) = 1 - x + x2/2

Answer 1

Part 1:

P₂(0.07)=0.93245≈
`e^(-0.07)`

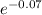
Part 2:

Error=
`0.5618*10^(-4)`

Explanation:

Given:

`f(x)=e^(x)\\f(-0.07)=e^(-0.07)`

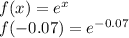
P₂(x)=
`1-x+(x^2)/(2)`

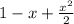
Solution:

Part 1:

P₂(x)=
`1-x+(x^2)/(2)`

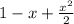
We have x=0.07

Put Value of x in above Equation:

P₂(0.07)=
`1-0.07+(0.07^2)/(2)`

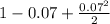
P₂(0.07)=0.93245≈
`e^(-0.07)`

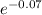
Part 2:

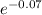`e^(-0.07)`=0.93239382 (Calculated using Calculator)

Error=|
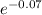`e^(-0.07)`-P₂(0.07)|=|0.93239382-0.93245|=0.00005618

Error=|0.93239382-0.93245|

Error=0.00005618

Error=
`0.5618*10^(-4)`