Explanation:
We first need to simplify the quadratic numerators and denominators. We'll use the fact that any equation of form
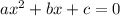
where it has solutions
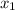 and
and
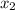 can be written as
can be written as
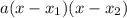
Where
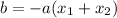 and
and
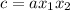
Fortunately, here a = 1 for all equations, so let's learn how to solve for a=1 because it's a bit simpler.
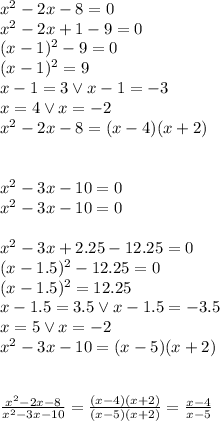
See, we've simplified the first term of the subtraction. Now let's do the same with the right side:
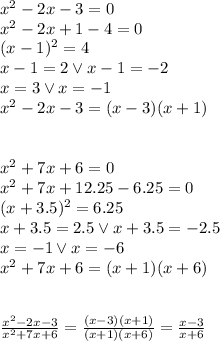
See, we've simplified the second term. Now we need to bring them to the common denominator:
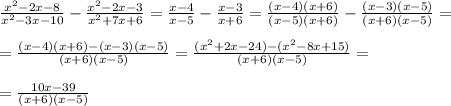
We could simplify even further if we can find some a and b so that
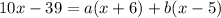
then
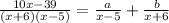
So let's try!
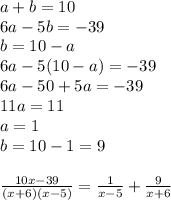
And that's the simplest form.