Question

 Find sin2x, cos2x, and tan2x if sinx=-15/17 and x terminates in quadrant III

Answer 1

Given:

`\sin x=-(15)/(17)`

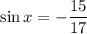
x lies in the III quadrant.

To find:

The values of
`\sin 2x, \cos 2x, \tan 2x`.

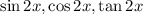Solution:

It is given that x lies in the III quadrant. It means only tan and cot are positive and others are negative.

We know that,

`\sin^2 x+\cos^2 x=1`

`(-(15)/(17))^2+\cos^2 x=1`

`\cos^2 x=1-(225)/(289)`

`\cos x=\pm\sqrt{(289-225)/(289)}`

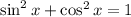
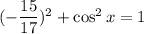
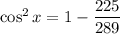
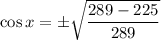
x lies in the III quadrant. So,

`\cos x=-\sqrt{(64)/(289)}`

`\cos x=-(8)/(17)`

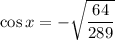
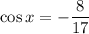
Now,

`\sin 2x=2\sin x\cos x`

`\sin 2x=2* (-(15)/(17))* (-(8)/(17))`

`\sin 2x=-(240)/(289)`

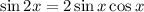
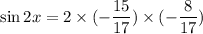
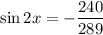
And,

`\cos 2x=1-2\sin^2x`

`\cos 2x=1-2(-(15)/(17))^2`

`\cos 2x=1-2((225)/(289))`

`\cos 2x=(289-450)/(289)`

`\cos 2x=-(161)/(289)`

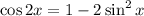
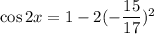
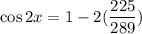
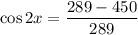
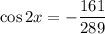
We know that,

`\tan 2x=(\sin 2x)/(\cos 2x)`

`\tan 2x=(-(240)/(289))/(-(161)/(289))`

`\tan 2x=(240)/(161)`

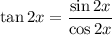
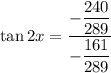
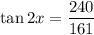
Therefore, the required values are
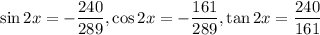`\sin 2x=-(240)/(289),\cos 2x=-(161)/(289),\tan 2x=(240)/(161)`.