Question

Find the least common multiple of 40a3bc and 28a2b4cd​

Answer 1

The least common multiple is
`280a^6b^4cd`

Explanation:

We find the least common multiple of the constant, and of each term.

Least common multiple of 40 and 28:

40 - 28|2

20 - 14|2

10 - 7|2

5 - 7|5

1 - 7|7

1 - 1

2*2*2*5*7 = 280

LCM of a^3 and a².

Exponents are 3 and 2.

LCM of 3 and 2 is 6. So

`a^6`

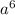
b and b^4

LCM of 1 and 4, which are the exponents, is 4. So

`b^4`

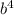
c and c

LCM of 1 and 1 is 1. So c

d

In the first term, no d means that it is
`d^0 = 1`

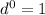
In the second,
`d^1 = d`

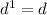
LCM of 0 and 1 is 1. So

d

Least common multiple:

Multiplication of all the LCM's. So

`280a^6b^4cd`