Answer:
The proposition is true.
Explanation:
Now we proceed to demostrate that expression given is true by algebraic means:
1)
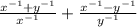 Given
Given
2)
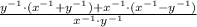
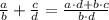
3)
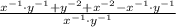 Distributive property/
Distributive property/
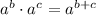
4)
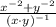 Commutative, associative and modulative properties/Existence of additive inverse/
Commutative, associative and modulative properties/Existence of additive inverse/
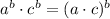
5)
![[(x\cdot y)^(-1)]^(-1)\cdot (x^(-2)+y^(-2))](https://img.qammunity.org/2022/formulas/mathematics/high-school/t11uzi5a0wcpr2anbdw563ygvw4julefs4.png) Commutative property/Definition of division
Commutative property/Definition of division
6)
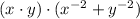
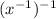
7)
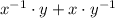 Distributive property/Associative property/
Distributive property/Associative property/
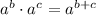
8)
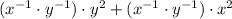 Modulative property/Existence of additive inverse/
Modulative property/Existence of additive inverse/
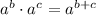
9)
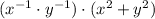 Distributive property
Distributive property
10)
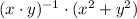
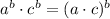
11)
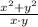 Commutative property/Definition of division/Result
Commutative property/Definition of division/Result