Question

A circle is drawn inside a square so its circumference touches each of the four sides of the square. If the area of the circle is 99.2cm2 calculate the length of the sides of the square.

Answer 1

The length of the sides of the square is approximately 11.239 centimeters.

Explanation:

Since the circle is inscribed in the square, the length of each side of the square (
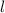`l`), in centimeters, is equal to the length of the diameter of the circle (
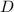`D`), in centimeters. The area of the circle (
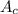`A_(c)`), in square centimeters:

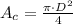`A_(c) = (\pi\cdot D^(2))/(4)` (1)

Where
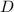`D` is the diameter of the circle, in centimeters.

If we know that
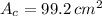`A_(c) = 99.2\,cm^(2)`, then the length of the sides of the square is:

`D = \sqrt{(4\cdot A_(c))/(\pi) }`

`l = D \approx 11.239\,cm`

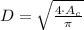
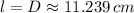
The length of the sides of the square is approximately 11.239 centimeters.