Question

A rocket is launched from a tower. The height of the rocket, y in feet, is

related to the time after launch, x in seconds, by the given equation. Using
this equation, find the maximum height reached by the rocket, to the nearest
tenth of a foot.
y = -16x2 + 212x + 139

Answer 1

y = 841.25 feet

Explanation:

Given that,

The height of the rocket, y in feet, is related to the time after launch, x in seconds, by the given equation as follows:

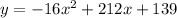`y = -16x^2 + 212x + 139` ....(1)

We need to find the maximum height reached by the rocket.

For maximum height, put dy/dx = 0

So,

`(d(-16x^2 + 212x + 139))/(dx)=0\\\\-32x+212=0\\\\x=(212)/(32)\\\\x=6.625\ s`

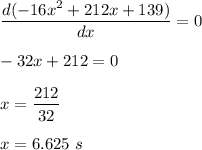
Pu x = 6.625 in equation (1).

`y = -16(6.625)^2 + 212(6.625) + 139\\\\y=841.25\ feet`

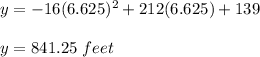
So, the maximum height reached by the rocket is equal to 841.25 feet.