Question

A culture started with 5000 bacteria after three hours it grew 6500 bacteria predict how many bacteria will be present after 13 hours round your answer to the nearest whole number

Answer 1

15595 bacteria will be present after 13 hours.

Explanation:

Continuous population growth:

The continuous population growth model, for the population after t hours, is given by:

`P(t) = P(0)e^(rt)`

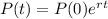
In which P(0) is the initial population and r is the growth rate.

Started with 5000 bacteria

This means that
`P(0) = 5000`

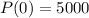
So

`P(t) = 5000e^(rt)`

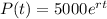
After three hours it grew 6500 bacteria:

This means that
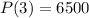`P(3) = 6500`. We use this to find r.

`P(t) = 5000e^(rt)`

`6500 = 5000e^(3r)`

`e^(3r) = (65)/(50)`

`\ln{e^(3r)} = \ln{(65)/(50)}`

`3r = \ln{(65)/(50)}`

`r = \frac{\ln{(65)/(50)}}{3}`

`r = 0.0875`

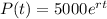
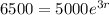
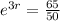
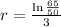
So

`P(t) = 5000e^(0.0875t)`

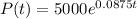
How many bacteria will be present after 13 hours?

This is P(13). So

`P(13) = 5000e^(0.0875*13) = 15594.8`

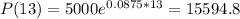
Rounding to the nearest whole number

15595 bacteria will be present after 13 hours.