Question

A student does an experiment with a string vibrating at 20 hertz and observes the resonance pattern shown in the

diagram:
What is the speed of the wave on the string in Figure 24-3A?
4.0 m/s
8.0 m/s
20 m/s
100 m/s

Answer 1

v = 8.0 m/s

Step-by-step explanation:

The diagram clearly shows that the string is vibrating in the 5th harmonic. Hence, the length of string in terms o wavelength can be given as:

`L = (5)/(2)\lambda\\\\\lambda = (2)/(5) L`

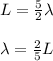
where,

λ = wavelength = ?

L = Length of string = 1 m

Therefore,

`\lambda = (2)/(5)(1\ m)\\\\\lambda = 0.4\ m`

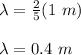
Now, the speed of the wave can be given by the following formula:

`v = f\lambda\\`

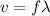
where,

v = speed of wave =?

f = frequency of wave = 20 Hz

Therefore,

`v = (20\ Hz)(0.4\ m)\\v = 8\ m/s\\`

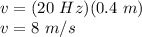
Hence, the correct answer is:

v = 8.0 m/s