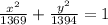Question

Write the standard form of an equation of an ellipse subject to the given conditions.

Endpoints of minor axis: (/37,0) and (-37,0);
Foci: (0,5) and (0, -5)
The equation of the ellipse in standard form is

Answer 1

The answer is below

Explanation:

The standard form of the equation of an ellipse with major axis on the y axis is given as:

`((x-h)^2)/(b^2) +((y-k)^2)/(a^2) =1`

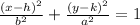
Where (h, k) is the center of the ellipse, (h, k ± a) is the major axis, (h ± b, k) is the minor axis, (h, k ± c) is the foci and c² = a² - b²

Since the minor axis is at (37,0) and (-37,0), hence k = 0, h = 0 and b = 37

Also, the foci is at (0,5) and (0, -5), therefore c = 5

Using c² = a² - b²:

5² = a² - 37²

a² = 37² + 5² = 1369 + 25

a² = 1394

Therefore the equation of the ellipse is:

`(x^2)/(1369)+ (y^2)/(1394) =1`