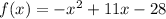Answer:
Explanation:
We see that the zeroes of the graphed parabola are
 and
and
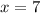 , which are solutions to
, which are solutions to
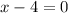 and
and
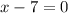 respectively. We also observe that the parabola opens downward, so the leading coefficient is negative. By multiplying these two factors and negating the result, we can determine the actual function:
respectively. We also observe that the parabola opens downward, so the leading coefficient is negative. By multiplying these two factors and negating the result, we can determine the actual function:
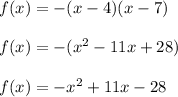
Thus, the quadratic equation represented by the graph is