Answer:
v = 0.99 c = 2.99 x 10⁸ m/s
Step-by-step explanation:
From the special theory of relativity:
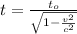
where,
v = speed of travel = ?
c = speed of light = 3 x 10⁸ m/s
t = time measured on earth = 90 years
t₀ = time measured in moving frame = 6 months = 0.5 year
Therefore,
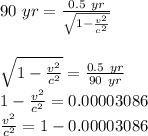
v = 0.99 c = 2.99 x 10⁸ m/s