Question

. In the casino game roulette, a wheel with 38 spaces (18 red, 18 black, and 2 green) is spun. In one possible bet, the player bets $1 on a single number. If that number is spun on the wheel, then they receive $36 (their original $1 $35). Otherwise, they lose their $1. On average, how much money should a player expect to win or lose if they play this game repeatedly

Answer 1

For each game, the player should be expected to lose $0.0263.

Explanation:

A probability is the number of desired outcomes divided by the number of total outcomes.

Probability of each outcome:

1/38 probability of winning, that is, 1/38 probability of receiving $36.

37/38 probability of losing, that is, 37/38 probability of losing $1.

On average, how much money should a player expect to win or lose if they play this game repeatedly?

For each game:

`E(X) = (1)/(38)*36 - (37)/(38)*1 = (36 - 37)/(38) = -(1)/(38) = -0.0263`

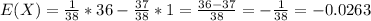
For each game, the player should be expected to lose $0.0263.