Question

Skid of weight 440 N is stuck in the middle of a circular frozen pond of radius 5 m. He cannot move because the pond is absolutely frictionless. He happens to have his 2.6 kg physics textbook so he looks for a solution to his problem. Unable to find a solution he throws his physics textbook in a fit a rage. Skid throws it at a velocity of 4 m/s directly away from him. After throwing the book, how long does it take Skid to reach the edge of the pond

Answer 1

It takes 21.7 seconds for Skid to reach the edge of the pond.

Step-by-step explanation:

We can calculate the time that takes Skid to reach the edge of the pond by conservation of linear momentum:

`p_(i) = p_(f)`

`m_(1)v_{1_(i)} + m_(2)v_{2_(i)} = m_(1)v_{1_(f)} - m_(2)v_{2_(f)}` (1)

Where:

m₁: is the Skid's mass

m₂: is the book's mass = 2.6 kg

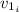`v_{1_(i)}`: is the initial speed of Skid = 0 (he was at rest)

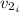`v_{2_(i)}`: is the initial speed of the book = 0 (it was at rest)

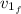`v_{1_(f)}`: is the final speed of Skid =?

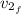`v_{2_(f)}`: is the final speed of the book = 4 m/s. This value is negative since it is moving in the opposite direction of Skid.

First, we need to calculate Skid's mass.

`m_(1) = (P)/(g)`

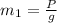
Where:

P: is the weight of Skid = 440 N

g: is the acceleration due to gravity = 9.81 m/s²

`m_(1) = (P)/(g) =(440 N)/(9.81 m/s^(2)) = 44.8 kg`

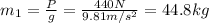
Now, we can find the speed of Skid from equation (1):

`0 = 44.8 kg*v_{1_(f)} - 2.6 kg*4 m/s`

`v_{1_(f)} = (2.6 kg*4 m/s)/(44.8 kg) = 0.23 m/s`

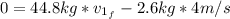
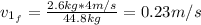
Finally, the time to reach the edge can be found by using the following equation:

`v_{1_(f)} = (d)/(t)`

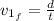
Where:

d: is the distance = radius = 5 m

t: is the time =?

`t = \frac{d}{v_{1_(f)}} = (5 m)/(0.23 m/s) = 21.7 s`

Therefore, it takes 21.7 seconds for Skid to reach the edge of the pond.

I hope it helps you!