Question

A survey conducted by the U.S. department of Labor found the 48 out of 500 heads of households were unemployed. Compute a 99% confidence interval for the proportion of unemployed heads of households in the population. Round to three decimal places. (make sure to type a zero in front of the decimal place ie. 0.1 vs .1 otherwise your answer will be marked incorrect) Lower limit

Answer 1

99% Confidence interval is given as;

Lower Limit = 0.062

Upper Limit = 0.130

Explanation:

Given the data in the question;

x = 48

n = 500

sample proportion p = x/n = 48/500 = 0.096

with 99% confidence

significance level ∝ = 1 - 99% = 1 - 0.99 = 0.01

∝/2 = 0.01 / 2 = 0.005

Critical Z-value =
`Z_{\alpha /2` =
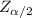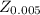`Z_{0.005` = 2.576

Now,

Standard error of p : SE = √[ (p × ( 1 - p) / n ) ]

we substitute

SE = √[ (0.096 × ( 1 - 0.096) / 500 ) ]

SE = √[ (0.096 × 0.904) / 500 ]

SE = √[ 0.086784 / 500 ) ]

SE = 0.0131745

so

Margin of Error E =
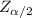`Z_{\alpha /2` × SE

E = 2.576 × 0.0131745

E = 0.0339

Now 99% confidence interval will be

⇒ 0.096 ± 0.0339

⇒ (0.096 - 0.0339, 0.096 + 0.0339 )

⇒ ( 0.062, 0.130 )

Lower Limit = 0.062

Upper Limit = 0.130