Answer:
0.2231 = 22.31% of customers having to hold more than 4.5 minutes will hang up before placing an order
Explanation:
Exponential distribution:
The exponential probability distribution, with mean m, is described by the following equation:
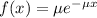
In which
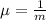 is the decay parameter.
is the decay parameter.
The probability that x is lower or equal to a is given by:
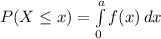
Which has the following solution:
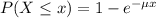
The probability of finding a value higher than x is:
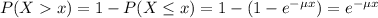
The length of waiting time was found to be a variable best approximated by an exponential distribution with a mean length of waiting time equal to 3 minutes.
This means that

What proportion of customers having to hold more than 4.5 minutes will hang up before placing an order?
This is:
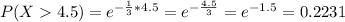
0.2231 = 22.31% of customers having to hold more than 4.5 minutes will hang up before placing an order