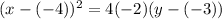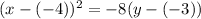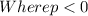Answer:
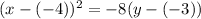

Explanation:
From the question we are told that:
Parabola focus co-ordinates
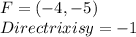
Generally the equation for standard form of Parabola is mathematically given by
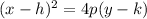
where p≠ 0
Generally the equation for Directrix of Parabola is mathematically given by
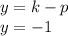
Generally the equation for Focus of Parabola F is mathematically given by
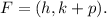
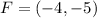
Therefore
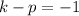
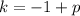
Given
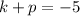
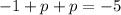
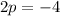
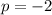
Therefore
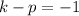
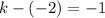
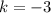
Generally the equation for standard form of Parabola is mathematically given by