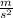Answer:
7.23407
Step-by-step explanation:
(I will not include units in calculations)
I'm assuming FBD's are already drawn, so I will work from there.
Let the 2.2kg block equal
 , and the 20kg block equal
, and the 20kg block equal
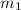 .
.
Summation equation for
 :
:
 ,
,
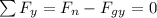
Summation equation for
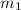 :
:

Torque Summation Equation:
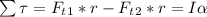
Do some plugging in with the values given:
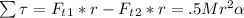
Replace
 with
with
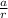 , and cancel out the r's.
, and cancel out the r's.
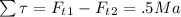
This step is important: Rearrange the force summation equation to solve for each tension force.

Perform Substitution:
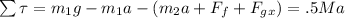
Now, we need to find the friction force and the horizontal component of the force of gravity.
Note that
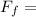 μ
μ
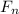
And based on our earlier summation equation:

First, break
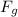 into x and y components.
into x and y components.
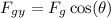 ,
,
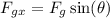
Perform substitution with this and the fact that
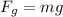 .
.
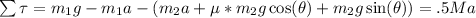
Solving for a, plugging in numbers yields an answer of 7.23407