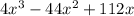Question

(1 point) An open-top box is to be constructed from a 8 \ \mbox{in} by 14 \ \mbox{in} rectangular sheet of tin by cutting out squares of equal size at each corner, then folding up the resulting flaps. Let x denote the length of the side of each cut-out square. Assume negligible thickness. (a) Find a formula for the volume, V, of the box as a function of x. \ \ V(x)

Answer 1

Volume=
`4x^3-44x^2+112x`

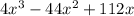
Explanation:

Let x denotes the length of the side of each cut

After Cutting square length will be=8-2x (where 2x for 2 squares as on each side two corners are there thus 2 squares will be cut down)

After cutting square width will be=14-2x (where 2x for 2 squares as on each side two corners are there thus 2 squares will be cut down)

Height = x

Volume=Length*width*Height

Volume=(8-2x)*(14-2x)*x

On solving we will get:

Volume=
`4x^3-44x^2+112x`