Answer:
The pvalue of the test is 0.0537 > 0.02, which means that there is not sufficient evidence to support the power company's claim at the 0.02 level of significance.
Explanation:
The U.S. Energy Information Administration claimed that U.S. residential customers used an average of 10,941 kilowatt hours (kWh) of electricity this year.
This means that the null hypothesis is:
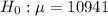
A local power company believes that residents in their area use more electricity on average than EIA's reported average.
This means that the alternate hypothesis is:
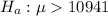
The test statistic is:

In which X is the sample mean,
 is the value tested at the null hypothesis,
is the value tested at the null hypothesis,
 is the standard deviation and n is the size of the sample.
is the standard deviation and n is the size of the sample.
10941 is tested at the null hypothesis:
This means that
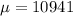
To test their claim, the company chooses a random sample of 115 of their customers and calculates that these customers used an average of 11,425kWh of electricity last year. The population standard deviation is of 3217kWh:
This means that
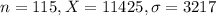
Value of the z-statistic:

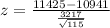

Pvalue of the test:
Probability of finding a mean above 11425, which is 1 subtracted by the pvalue of z = 1.61.
Looking at the z-table, z = 1.61 has a pvalue of 0.9463.
1 - 0.9463 = 0.0537
The pvalue of the test is 0.0537 > 0.02, which means that there is not sufficient evidence to support the power company's claim at the 0.02 level of significance.