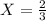Answer:
a)
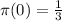
b)
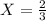
Explanation:
From the question we are told that:
Arrival time with Poisson's process =
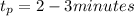
where
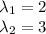
a)
Generally the equation Poisson's process is mathematically given by

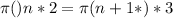
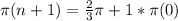
Therefore
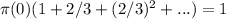
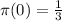
The proportion of arriving customers that get taxis.
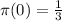
b)
Generally the average number of taxis X waiting is mathematically given by