Question

A proton is moving in a circular orbit of radius 20 cm under a uniform magnetic field 0.3 t perpendicular to the velocity of the proton then the velocity of this pronto

Answer 1

v = 5.75 x 10⁶ m/s

Step-by-step explanation:

The radius (r) of the circular orbit taken by a charged particle is related to its speed perpendicular to a magnetic field of strength B, and is given by

r =
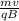`(mv)/(qB)` --------------(i)

Where,

q = charge of the particle

m = mass of the particle

Making v subject of the formula in equation (i) above gives

v =
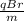`(qBr)/(m)` -------------------(ii)

Given;

r = 20cm = 0.2m

B = 0.3T

v = unknown

q = charge of proton = 1.6 x 10⁻¹⁹ C

m = mass of the proton = 1.67 x 10⁻²⁷kg

Substitute the values of m, q, B and r into equation (ii) above to get;

v =
`\frac{1.6 * 10^(-19) * 0.3 * 0.2} {1.67*10^(-27) }`

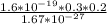
Solving for v gives:

v = 5.75 x 10⁶ m/s

Therefore, the velocity of the proton is 5.75 x 10⁶ m/s