Question

The average size of a new house built in a Hays county in 2010 was 1,872 square feet. A random sample of 40 new homes built in Hays County were selected in 2014. The average square footage was 2,031 with a standard deviation of 373 square feet. Does this sample provide enough evidence to conclude that the average house size has increased in the Hays County since 2010? Test at an alpha level of 0.05. Find the test statistic.

Answer 1

The test statistic is z = 2.7.

The pvalue of the test is 0.0035 < 0.05, which means that this sample provides enough evidence to conclude that the average house size has increased in the Hays County since 2010.

Explanation:

The average size of a new house built in a Hays county in 2010 was 1,872 square feet. Evidence that it has increased?

This means that the null hypothesis is:

`H_0: \mu = 1872`

And the alternate hypothesis is:

`H_a: \mu > 1872`

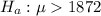
The test statistic is:

`z = (X - \mu)/((\sigma)/(√(n)))`

In which X is the sample mean,
`\mu` is the value tested at the null hypothesis,
`\sigma` is the standard deviation and n is the size of the sample.

1872 is tested at the null hypothesis:

This means that
`\mu = 1872`

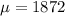
Sample of 40. The average square footage was 2,031 with a standard deviation of 373 square feet.

This means that
`n = 40, X = 2031, \sigma = 373`

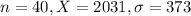
Value of the test-statistic:

`z = (X - \mu)/((\sigma)/(√(n)))`

`z = (2031 - 1872)/((373)/(√(40)))`

`z = 2.7`

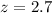
Pvalue and decision:

The pvalue of the test is the probability of finding a sample mean above 2031. This is 1 subtracted by the pvalue of z = 2.7.

Looking at the z-table, z = 2.7 has a pvalue of 0.9965

1 - 0.9965 = 0.0035

The pvalue of the test is 0.0035 < 0.05, which means that this sample provides enough evidence to conclude that the average house size has increased in the Hays County since 2010.