Question

Solve using log
Help would be much appreciated

Answer 1

`10^(x-3.6)-7=41`

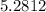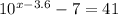
Use the rules of exponents and logarithms to solve the equation.

`10^(x-3.6)-7=41`

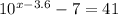
Add 7 to both sides of the equation.

`10^(x-3.6)=48`

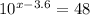
Take the logarithm of both sides of the equation.

`log(10^(x-3.6))=log(48)`

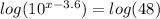
The logarithm of a number raised to a power is the power times the logarithm of the number.

`(x-3.6)log(10)=log(48)`

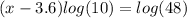
Add 3.6 to both sides of the equation.

`x=log(48)-(-3.6)`

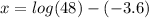
Solve by first finding
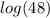`log(48)` then subtract
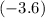`(-3.6)` from the answer:

1.
`log(48)=1.6812412373755872181499834821531`

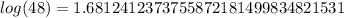
Now just solve the equation:

`1.6812412373755872181499834821531 - (-3.6)=5.2812412373755872181499834821531`

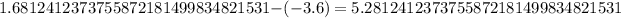
Your answer is C.
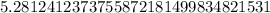`5.2812412373755872181499834821531` or
`5.2812`

Answer 2

5.2812

Explanation:

`10^(x-3.6)-7=41`

Add 7 to both sides:

`\implies 10^(x-3.6)=48`

Taking logs of base 10:

`\implies \log_(10)10^(x-3.6)=\log_(10)48`

Apply log rule
`\log a^b=b \log a`:

`\implies (x-3.6)\log_(10)10=\log_(10)48`

Apply log rule
`\log_aa=1`:

`\implies (x-3.6)* 1 =\log_(10)48`

Simplify and solve:

`\implies x-3.6=\log_(10)48`

`\implies x=\log_(10)48+3.6`

`\implies x = 5.281241237...`