Question

Can anyone help please????

Answer 1

Option A.
`(f_of^(-1))(-2)=-2`

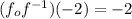
Explanation:

Point to remember while solving the question of function,

`(f_of^(-1))(x)=x`

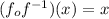
Here, 'f' is the parent function and
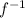`f^(-1)` is the inverse of the function 'f'.

So for the given function,

f(x) = 2x - 2

`(f_of^(-1))(x)=x`

For x = -2

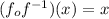
`(f_of^(-1))(-2)=(-2)`

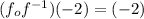
Therefore, Option A will be the correct answer.