Question

Two small nonconducting spheres have a total charge of 94.0 μC . Part A

When placed 31 cm apart, the force each exerts on the other is 11.5 N and is repulsive. What is the charge on each?

Q1,Q2=


Part B

What if the force were attractive?

Q1,Q2=

Answer 1

Part A;

The charges are;

Q₁ = 1.32687 μC and Q₂ = 92.67313 μC

Part B

Q₁ = 95.29042 μC, Q₂ = -1.29042 μC

Step-by-step explanation:

Part A

The total charge on the two nonconducting spheres = 94.0 μC

The force exerted by each on the other when placed 31 cm apart = 11.5 N

Let Q₁ = x represent the charge on one of the spheres and let Q₂ represent the charge on the other sphere

The force, 'F', exerted by a charge is given as follows;

`F = k * (\left | Q_1 \right | \cdot \left | Q_2 \right | )/(d^2)`

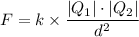
Where;

d = The distance between the spheres = 31 cm = 0.31 m

k = 8.9875 × 10⁹ N·m²/C²

Where F = 11.5 N

Q₁ + Q₂ = 94.0 μC

∴ Q₂ = 94.0 - Q₁ = 94.0 - x

We get;

`F =11.5 = 8.9875 * 10^9 * (x* (94.0-x) * 10^(-12))/(0.31^2)`

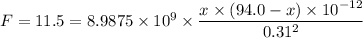
Therefore;

94·x - x² - 122.965 = 0

x² - 94·x + 122.965

x = (94 ± √((-94)² - 4×1×122.965))/(2 × 1)

Solving gives;

x ≈ 1.32687 × 10⁻⁶ C or x = 92.67313 × 10⁻⁶ C

Therefore, the charges are;

Q₁ = 1.32687 × 10⁻⁶ C and Q₂ = 92.67313 × 10⁻⁶ C

Q₁ = 1.32687 μC and Q₂ = 92.67313 μC

Part B

For attractive force, we have;

Q₁ + Q₂ = 94 × 10⁻⁶...(1)

`11.5 = 8.9875 * 10^9 * (-x* (94.0-x))/(0.31^2) = 8.9875 * 10^9 * (-Q_1* Q_2)/(0.31^2)`

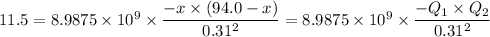
-Q₁ × Q₂ = 11.5 × 0.31²/(8.9875 × 10⁹) = 1.2296523 × 10⁻¹⁰...(2)

∴ Q₂ = -1.2296523 × 10⁻¹⁰/(Q₁)

Q₁ + Q₂ = Q₁ - 1.2296523 × 10⁻¹⁰/(Q₁) = 94 × 10⁻⁶

Q₁² - 94 × 10⁻⁶·Q₁ - 1.2296523 × 10⁻¹⁰ = 0

∴ Q₁ = (94 × 10⁻⁶ ± √((-94 × 10⁻⁶)² - 4 × 1 × 1.2296523 × 10⁻¹⁰))/(2×1)

Q₁ = 9.529042 × 10⁵ C or -1.29042 × 10⁻⁶ C

Therefore, Q₁ = 9.529042 × 10⁵ C and Q₂ = -1.29042 × 10⁻⁶ C

Q₁ = 95.29042 μC and Q₂ = -1.29042 μC