Answer:
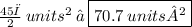
______________________
The correct option is 70.7
Explanation:
Since the green and red make a semicircle, the total measure must be 180°.
Since the two green sectors are both 40°.
The red must add up with the green sectors to total 180°.
This means that:
red sector + 80° = 180°.
–80° –80.
red sector = 100°.
To find the area of a sector, we must first understand the area of the circle itself which is πr², where r is the radius.
Since a full circle is 360°.
(360° / 360°)( πr² ) will be the area.
Or in radians: (2π rad / 2π rad)( πr² ).
From here, we can create the formula:
Area of a sector = ( n° / 360° ) ( πr² ). Where n is the measure or the sector in degrees, and r is the radius.
You may also know that the diameter is twice the measure of the radius.
This means that if we are given a diameter of 18 units from the problem, the radius will be 18/2 or 9 units.
Lastly, all we have to do is substitute all this information to find the area of sector.
Area of the red sector = ( n° / 360° ) ( πr² ).
Area of the red sector =
( (100°) / 360° ) ( π(9)² ).
Area of the red sector = ( 5 / 18 ) ( 81π )
Area of the red sector = ( (5)(81π) / 18 )
Area of the red sector = ( (405π) / 18 )
Area of the red sector = ( 45π / 2 ) units²
Area of the red sector =
(141.371669412.. units²) / 2
Area of the red sector =
70.6858347058.. units²
Area of the red sector ≈
70.7 units²