Question

as an aid in understanding this problem. The drawing shows a positively charged particle entering a 0.61-T magnetic field. The particle has a speed of 230 m/s and moves perpendicular to the magnetic field. Just as the particle enters the magnetic field, an electric field is turned on. What must be the magnitude of the electric field such that the net force on the particle is twice the magnetic force

Answer 1

E = 420.9 N/C

Step-by-step explanation:

According to the given condition:

`Net\ Force = 2(Magnetic\ Force)\\Electric\ Force - Magnetic\ Force = 2(Magnetic\ Force)\\Electric\ Force = 3(Magnetic\ Force)\\qE = 3qvBSin\theta\\E = 3vBSin\theta`

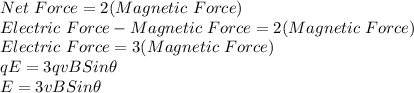
where,

E = Magnitude of Electric Field = ?

v = speed of charge = 230 m/s

B = Magnitude of Magnetic Field = 0.61 T

θ = Angle between speed and magnetic field = 90°

Therefore,

`E = (3)(230\ m/s)(0.61\ T)Sin90^o`

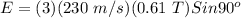
E = 420.9 N/C