Question

Question 15 (5 points)
Find the angle between u = <7, -2> and v= (-1,2>.

Answer 1

Approximately
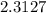`2.3127` radians, which is approximately
`132.51^(\circ)`.

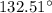Explanation:

Dot product between the two vectors:

`\begin{aligned}& u\cdot v \\ =\; & 7 * (-1) + (-2) * 2 \\ =\; & (-11) \end{aligned}`.

Magnitude of the two vectors:

`\begin{aligned} \| u \| &= \sqrt{{7}^(2) + {(-2)}^(2)} \\ &= √(53) \end{aligned}`.

`\begin{aligned} \| v \| &= \sqrt{{(-1)}^(2) + {2}^(2)} \\ &= √(5) \end{aligned}`.

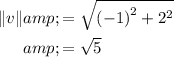Let
`\theta` denote the angle between these two vectors. By the property of dot products:

`\begin{aligned} \cos(\theta) &= (u \cdot v)/(\|u\| \, \| v \|) \\ &= ((-11))/((√(53))\, (√(5))) \\ &= ((-11))/(√(265))\end{aligned}`.

Apply the inverse cosine function
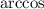`{\rm arccos}` to find the value of this angle:

`\begin{aligned} \theta &= \arccos\left((u \cdot v)/(\| u \| \, \| v \|)\right) \\ &= \arccos\left(((-11))/(√(265))\right) \\ & \approx \text{$2.3127$ radians} \\ &= 2.3127 * (180^(\circ))/(\pi) \\ &\approx 132.51^(\circ)\end{aligned}`.