Answer:
 , which is equal to
, which is equal to
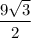 .
.
Explanation:
An angle of
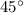 corresponds to an isosceles right triangle: the length of the two legs (adjacent and opposite) would be equal. Accordingly:
corresponds to an isosceles right triangle: the length of the two legs (adjacent and opposite) would be equal. Accordingly:
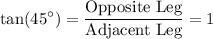 .
.
Let
 denote the measure of an angle. Double-angle identity for sine:
denote the measure of an angle. Double-angle identity for sine:
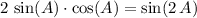 .
.
By this identity:
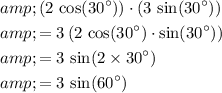 .
.
(
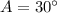 in this instance.)
in this instance.)
Hence:
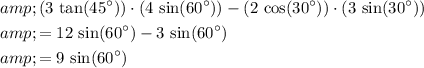 .
.
 . Therefore,
. Therefore,
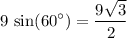 .
.